1　時空の幾何学　この頁

2　いざ、プリンシベ島へ　

・・・

ニュートンの重力理論では、重力場は「重力ポテンシャル」とよばれる、たった1個の量であたえられる。 質量がmとMの 2物体が r の距離にあるとき、重力ポテンシャル U は、

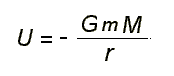
であらわされる。Gは重力定数であり、 距離 r が定まれば、その場所における重力場は１個の定数 であたえられることがわかる。ではアインシュタインが考察する4次元の時空間での重力場はどうすれば計算できるのか。じつは リーマンの計量テンソルがそのまま重力ポテンシャルとして利用できることに、アインシュタインは気がついた。4次元の時空間 のなかのある“点”における幾何学的特性を規定する計量テンソルが、そのままその場所での重力を規定する量として利用できる ことになったわけだから、きわめて大きな前進だ。ここからスタートして、一般共変性を保ちつつ計量テンソルを操作して、 最終的な重力場の方程式を発見すればいい。だがそれは楽な道のりではなかった。高等数学に不慣れなアインシュタインは、親友の グロスマンの助けを借りて、まず一般相対性理論に必要な数学から学ばなければならなかったのだ。重力による光線の曲がりを 検証する日食観測の準備に奔走しながら、理論の面では試行錯誤を繰りかえし、いったんは手に入れかけた正解から遠ざかるという、 彼らしからぬ回り道もした。ついに1914年11月には最終版と自負する論文を書きあげたのだが、これに賛同する物理学者は いなかった。

1915年11月4日木曜日、アインシュタインはベルリンのプロイセン科学アカデミーで「一般相対性理論について」と題した 論文を読み上げた。その冒頭、かれは前年秋に公表した重力場の方程式は誤りだと認め、一般共変性を重力の理論の出発点 とすべきことを明言する。グロスマンとの共同研究でえられた1914年の方程式は、一般共変性を断念することでみちびかれた もので、それはアインシュタインが宇宙のどこでも通用する重力方程式を書くのをあきらめたことを意味していた。ところがいま、 3年前に捨てさった「一般共変性」にたちもどって前年の論文を検討してみると、論理の見通しがよくなって、より単純化された 方程式があらわれてくる。重力場の方程式もすっきりしたかたちとなって、しかもその近似にはニュートン方程式がふくまれていた。 さらに翌週11日の発表では、きわめて大胆な仮説を導入することで、ある特別な座標系では一般共変な方程式がみちびかれる ことがしめされた。重力を幾何学化するという大目標まで、アインシュタインはあと2週間のところまでせまっていた。

当時、ドイツの数学研究の中心だったゲッティゲン大学の教授で、20世紀最大の数学者のひとりとされるダーフィト・ヒルベルト （1862〜1943）は、つぎのように語ったという。

《ゲッティゲンの道を歩いている誰をつかまえてもアインシュタインよりも四次元 空間についてよく理解している。・・・ところが、それにもかかわらず、あのような仕事をやったのはアインシュタインであって、 数学者ではなかった》

また別の機会には、《何故に、われわれの世代でアインシュタインが空間と時間についてのもっとも独創的で深い言葉を いい得たのでしょうか？それは、彼が時間および空間についての哲学と数学について何一つ学ばなかったからです！》とものべている。 アインシュタインは数学者ではなかったけれど、物理の研究に数学が必要とされる局面では、たくみに数学をあやつることができた。 一般相対性理論の完成にいたるプロセスは、そのもっとも端的な例といっていい。

11日の発表の時点で、おそらくアインシュタインは、新しい方程式が論理的に整合性がとれていることに強い自信をもっていた。 だが論理が万人に受けいれられるためには、なによりもまず、その方程式が正しく自然を記述しているかどうかを検証する必要がある。 自然のことは自然に聞け―アインシュタインは、二つの事例について計算を試み、その結果に大いに満足した。

第一は、水星の近日点移動の観測値を完全に説明できたこと。近日点とは、惑星の公転軌道（楕円軌道）の太陽にいちばん 近い点をいい、長い年月のあいだにはその位置を変える。太陽にもっとも近い水星では100年間に43秒（1度の60分の43）の変化が 観測されていたが、ニュートン力学ではこの数値は説明できず、そこで水星のさらに内側にある未知の惑星ヴァルカンの影響だと 考える天文学者もいた。近日点の移動は、近傍の惑星の影響が原因だと考えられていたわけだが、一般相対性理論は、惑星の作用 がなくても、近日点が移動することを予測する。しかもアインシュタインが新たにみちびいた方程式で計算してみると、観測値と みごとに一致する答えが得られたのだ。《私はうれしさのあまり数日間ぼうっとしていました》とアインシュタインは、後日、 友人パウル・エーレンフェストにあてた手紙に書いている（1916年1月17日付）。

第二の収穫は、太陽の重力場による光の曲がりの数値について、自らの誤りを発見したこと。以前の予測値は、光を粒子 すなわち光量子<光子>とみなし、この粒子が質量をもつと仮定してみちびいたものだった。つまりニュートンの平坦な3次元空間 を飛ぶ光子の軌跡の曲がりぐあいを算出したわけだが、一般相対性理論では、曲がっているのは空間であり、光ではない。新しい 方程式があたえた数値は、以前の値のちょうど2倍になった。日食の観測でこの値が確認されれば、一般相対性理論の正しさが証明 されることになる。

11月18日、アインシュタインは、水星の近日点移動についての成果をアカデミーで発表し、さらに1週間後の11月25日、 「重力場の方程式」と題した論文をアカデミーの物理数学分科会で読みあげた。難産だった一般相対性理論が、ついに完成した のだ。

アインシュタインがたどりついた重力場の方程式は、どのような座標系においても理論が形を変えないという 「一般座標系変換に対する不変性」を保証しつつ、時空の本質をこのうえなくエレガントに、簡潔に記述している。

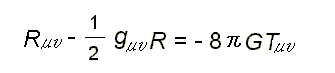
方程式は三つのテンソルの項からなっており、物質のエネルギー・運動量テンソル 《Tμυ》 によって、重力場をあらわす計量テンソル 《gμυ》 がきまることを示している。 《Rμυ》 は時空の形状をあらわすリッチ・テンソル、 Rはスカラー曲率、Gはニュートンの重力定数だ。