物理の窓
ガリレオの落体運動の実験と論証
3 動いている物体は永久に動きつづける
それでは『天文対話』の慣性問答に入りましょう。
先ずサルヴィアチがシンプリチオに質問します。以下はその問答です。
「いま鏡のように滑らかな面を考える。そして、
それを地平面に平行ではなく、少し傾いておく、その上に青銅のような重くて硬い球をのせて手をはなす。
そうするとその球はどうなるか」
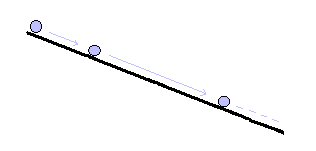
斜面がつづくかぎり無限に、
そして加速しながら
低いほうへ運動はつづくだろう
低いほうへ運動はつづくだろう
「低く傾いている方向に球は自分で動きだすだろう」
「ではどんな速さでどれだけ動くか。ただし空気の抵抗や
その他あらゆる外的障害はないとして。」
「球は傾斜がつづくかぎり無限に、そして加速しながら
低いほうへ運動はつづく。なぜなら低い位置につくのは重さを持った物体の本性だから」というアリストテレス派の理由を
つけ加える。
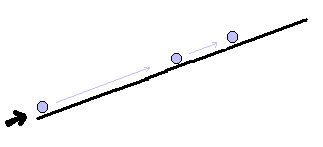
球は上むきに動くけれどもそれは暴力によって
強制された運動だから、だんだん遅くなるだろう
強制された運動だから、だんだん遅くなるだろう
「では、その同じ面上で球を高いほうに弾(はじ)いたら
どうなるだろう。」
「そうすれば球は上むきに動くけれどもそれは暴力によって
強制された運動だから、だんだん遅くなるだろう」
そこでサルヴィアチは次に質問をします。
「それでは上下いずれにも傾いていない面の上では
どうなるか答えてください」
「下方に傾いていないのですから運動への自然的傾向はないし、
また上方に傾いてもいないのですから動くことに抵抗もありません。だから、運動への推進と抵抗の間でどちらにも偏らないわけで、
結局は自然にじっとしておらねばならないでしょう」
この答えには次の質問が待っています。
「球をそこにそっと置くときはそうでしょう。
しかしどちらかの方向に球を弾(はじ)いたらどうなるでしょうか」
「その方向に球は動いて行くでしょう」
「それはどういう運動ですか。下方に傾いている面上
でのように加速運動ですかそれとも上方に傾いている面上でのように減速運動ですか」
「加速の原因も減速の原因も見出されません。
上方へも下方へも面は傾いていないのですから」
そこでサルヴィアチは質問します。
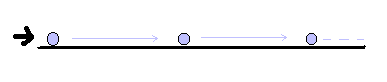
摩擦のない完全な平面上では、減速の原因がない限り、
また外的障害がない限り、動いている物体は 永久に動き
つづけるだろう
また外的障害がない限り、動いている物体は 永久に動き
つづけるだろう
「そうです。しかも減速の原因がないなら、
まして静止の原因もありません。それで君はその球がどれだけ運動をつづけると思いますか」
そうしてシンプリチオの次の答えを引き出します。
「上下どちらにも傾いていないその面の長さがつづくかぎりです」
このような論法で、減速の原因がない限り、また外的障害がない限り、動いている物体は永久に動きつづける、ということを
シンプリチオに納得させようとしました。でも、ガリレオは宗教裁判にかけられたとき「それでも地球は動く」といったとか。
シンプリチオも「それでも物体は止まる」と思ったかどうか。
しかしこの意味での「慣性法則」は、今日意味するものと同じではないともいえます。すなわち、上下いずれにも傾いていない
面と彼がいうのは、実は平面ではなく、地球の地平面に平行な同心球面のことなのです。ですから、彼の意味での慣性運動は円運動
であって、後にニュートンがはっきりさせ、われわれが学校で習ったような直線運動ではない。
そもそも『天文対話』のはじめの箇所でも、彼はサルヴィアチの口を借りて、直線運動が無限の長さを要求する、という理由で
それを拒否しているのです。このような直線の拒否や円の偏重はアリストテレスの考えたことでありますから、その点でガリレオも
この古い哲学者の呪縛からまだ十分解放されていなかったようです。しかし、一方、力の補充がなければ物体の運動は停止する、
という古い考えから一歩踏み出したことはガリレオの大きな功績です。
更新2009年1月29日